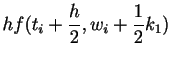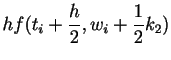Runge Kutta

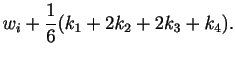The Runge Kutta methods provide further systematic improvement in the spirit of the modified Euler method. Because of their simplicity and accuracy, they are some of the most popular methods for integrating ordinary differential equations.

For example, the fourth order Runge Kutta method does four function evaluations per step to give a method with fourth order accuracy. We state the stepping method without proof:

$$k_1 = h f(t_i,w_i)$$

$$k_2 = h f(t_i + \frac{h}{2}, w_i + \frac{1}{2}k_1)$$

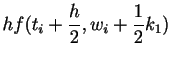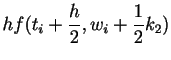$$k_3 = h f(t_i + \frac{h}{2}, w_i + \frac{1}{2}k_2)$$ (7)

$$k_4 = h f(t_{i+1}, w_i + k_3)$$ (8)

$$w_{i+1} = w_i + \frac{1}{6}(k_1 + 2 k_2 + 2 k_3 + k_4).$$

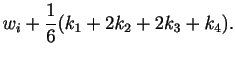Notice that the first two steps look like the modified Euler method for reaching the midpoint $t = t_i + h/2$. We leave as an exercise for the student to rewrite the modified Euler method in the $k_i$ notation above. Of course $k_2$ in that case has to be evaluated at $t_i+h$.

There are many Runge Kutta methods of different order. The second order Runge Kutta method is also called the midpoint method and goes like this:

$$k_1 = h f(t_i,w_i)$$

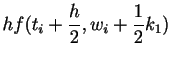$$k_2 = h f(t_i + \frac{h}{2}, w_i + \frac{1}{2}k_1)$$ (9)

$$w_{i+1} = w_i + k_2.$$

Like the modified Euler method, it is second order.

Probably because for many problems it gives a good compromise between the limitations of complexity, which argue for not going to too high order, and the benefits of accuracy, which argue for higher order, the fourth order method is especially popular.