


Next: Modified Euler Method
Up: ode
Previous: ode
The ordinary differential equation
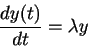 |
(1) |
with initial condition 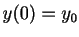 has the solution
has the solution
Let's call the independent variable ``time''. A numerical approach to
the solution starts from the initial time 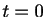 and steps forward in
discrete time steps
and steps forward in
discrete time steps 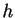 , namely
, namely 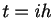 for
for
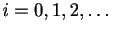 .
Let
.
Let 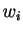 denote the approximation to
denote the approximation to 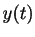 at
at 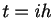 . To step
forward in time we begin with the finite-difference representation of
the derivative, namely,
. To step
forward in time we begin with the finite-difference representation of
the derivative, namely,
Using this approximation in the equation gives
or
This is a recursion relation (also called a difference equation),
allowing us to step the approximate solution forward in time, starting
at 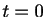 with
with 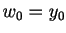 . The solution is
. The solution is
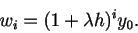 |
(2) |
In order for this result to be a good approximation, we require that
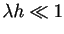 , in which case
, in which case
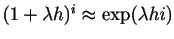 .
.
The method outlined above is called the Euler method. The more
general problem to be solved is
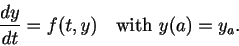 |
(3) |
Usually we are interested in the solution 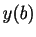 at
at 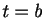 . So we
divide the time interval
. So we
divide the time interval ![$[a,b]$](img21.gif) into
into 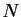 steps and write
steps and write
for
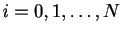 , where
, where
Again we denote the approximate solution as 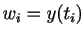 and
approximate the first derivative as a simple (forward) finite
difference. The Euler method then gives the recursion relation
and
approximate the first derivative as a simple (forward) finite
difference. The Euler method then gives the recursion relation
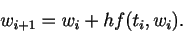 |
(4) |
Let's see how the approximation to 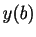 improves as
improves as 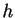 is
decreased. To see this we consider the error in the finite difference
approximation to the derivative. A Taylor's series expansion gives
is
decreased. To see this we consider the error in the finite difference
approximation to the derivative. A Taylor's series expansion gives
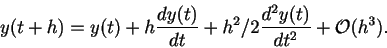 |
(5) |
The finite difference approximation we used above amounts to dropping
the terms in 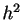 and higher powers of
and higher powers of 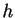 on the rhs. Putting
on the rhs. Putting 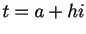 and using the ODE then gives the difference equation
and using the ODE then gives the difference equation
The Euler method truncates the series after the second term on the
rhs. We see that the error made in such an approximation scales with
the square of the step size. So if we decrease the step size by a
factor of 2 the Euler error in a single step decreases by a factor of
4. Notice, however, that we must then take twice as many steps to
reach 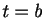 . So the net error decreases by a factor of two when the
step size is decreased by a factor of two.
. So the net error decreases by a factor of two when the
step size is decreased by a factor of two.
We call the error in the difference equation the local truncation
error to distinguish it from the global error in the final result
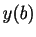 . More generally, with a local truncation error of
. More generally, with a local truncation error of  in each step and
in each step and 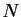 steps, the global error in
steps, the global error in 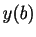 is
is
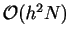 or
or
![${\cal O}[h(b-a)]$](img34.gif) . Since
. Since 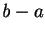 is constant, the
error in
is constant, the
error in 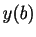 is linear in
is linear in 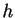 , as we have seen.
, as we have seen.
When the error in a method decreases as the first power of 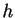 we call
it a first order method. The Euler method is therefore a first
order method.
we call
it a first order method. The Euler method is therefore a first
order method.



Next: Modified Euler Method
Up: ode
Previous: ode
Carleton DeTar
2008-12-01
![]() improves as
improves as ![]() is
decreased. To see this we consider the error in the finite difference
approximation to the derivative. A Taylor's series expansion gives
is
decreased. To see this we consider the error in the finite difference
approximation to the derivative. A Taylor's series expansion gives
![]() . More generally, with a local truncation error of
. More generally, with a local truncation error of ![]() in each step and
in each step and ![]() steps, the global error in
steps, the global error in ![]() is
is
![]() or
or
![]() . Since
. Since ![]() is constant, the
error in
is constant, the
error in ![]() is linear in
is linear in ![]() , as we have seen.
, as we have seen.
![]() we call
it a first order method. The Euler method is therefore a first
order method.
we call
it a first order method. The Euler method is therefore a first
order method.